A/B testing is a very popular topic among companies. You can find my workflow in A/B Testing Project, which contains an A/B testing example by using Tableau. However, real-life problems are usually more complicated. If an A/B testing experiment has multiple treatment groups, the cost of testing each treatment group and the probability of false positives will increase. When there are multiple treatments groups, I usually use two types of reinforcement learning, Upper Confidence Bound (UCB) Algorithm and Thompson Sampling to quickly find out the best treatment group by using the minimum amount of time. Multi-armed bandit problem is a problem in which a fixed limited set of resources must be allocated between competing (alternative) choices in a way that maximizes their expected gain, when each choice's properties are only partially known at the time of allocation, and may become better understood as time passes or by allocating resources to the choice.
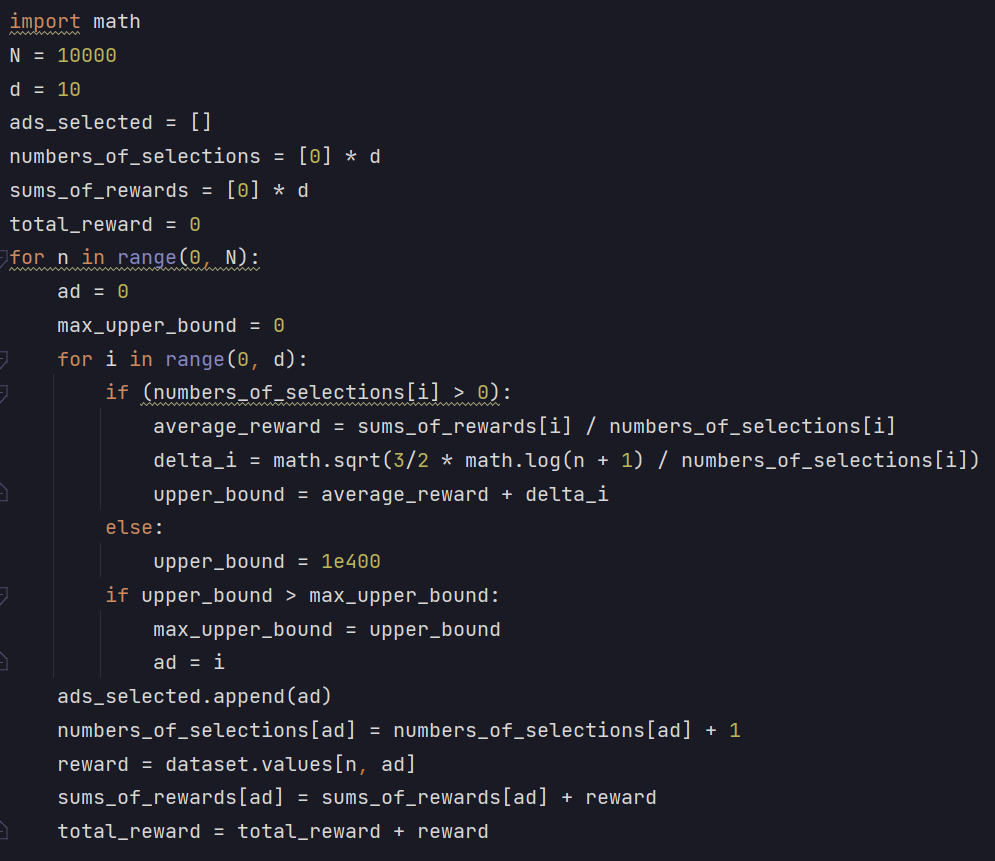
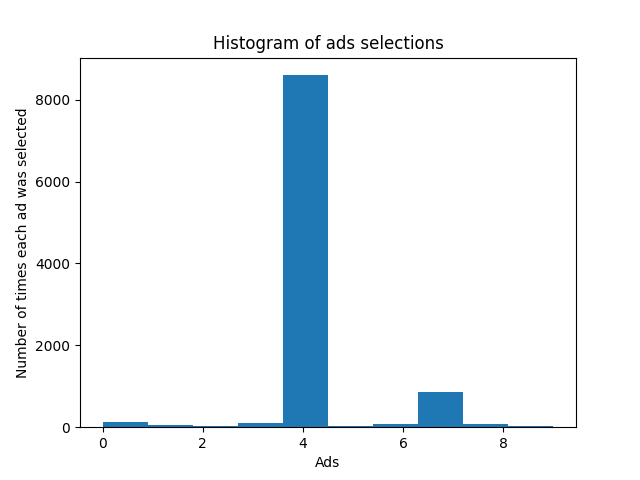
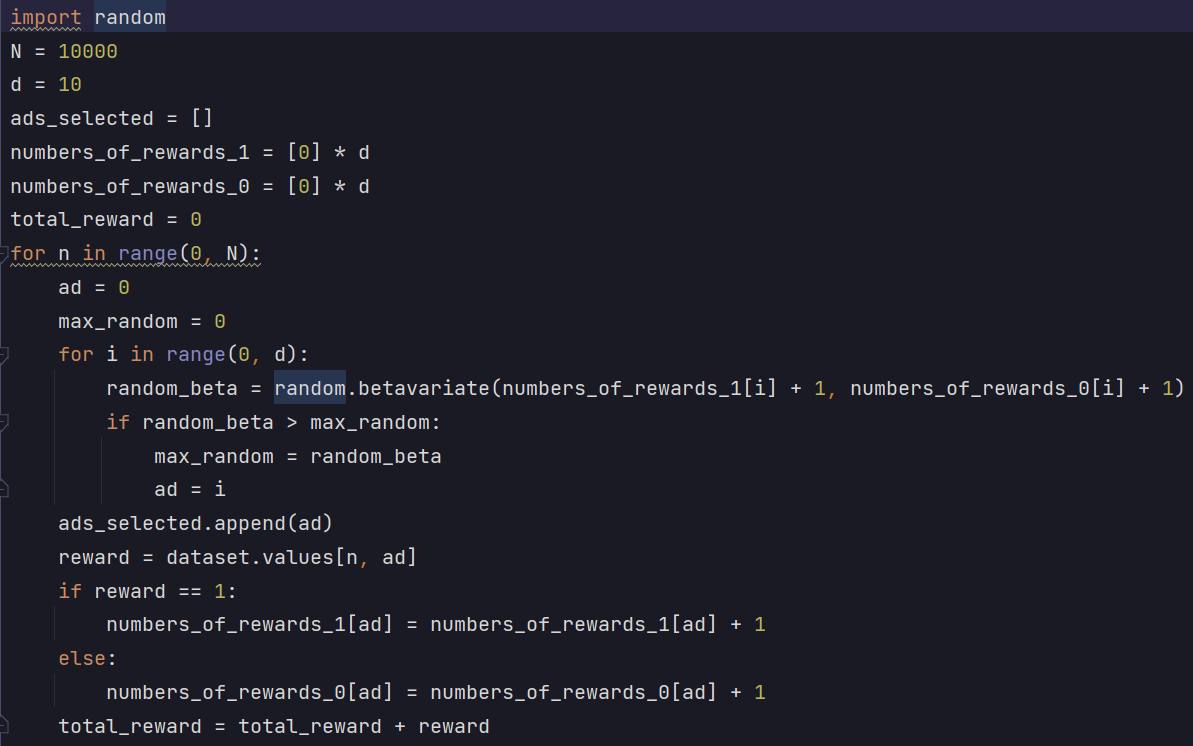
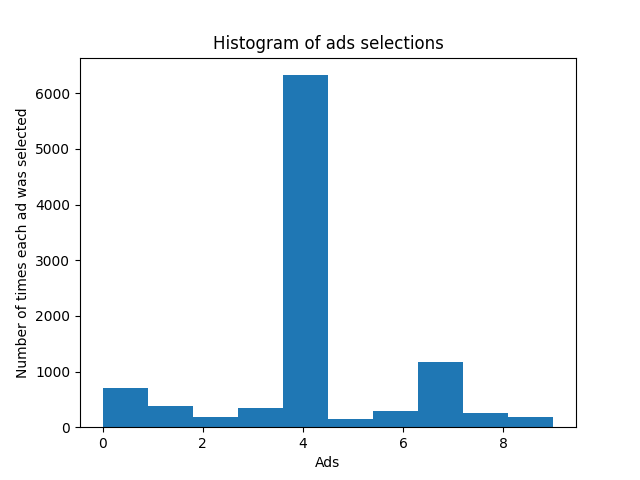
In marketing terms, a multi-armed bandit solution is a 'smarter' or more complex version of A/B testing that uses machine learning algorithms to dynamically allocate traffic to variations that are performing well, while allocating less traffic to variations that are underperforming. The images below show the simplified process of my Upper Confidence Bound (UCB) Algorithm and Thompson Sampling models. Each model was run 10000 rounds and Thompson Sampling performed better.